決定木分析 (Decision Tree Analysis) は、機械学習の手法の一つで決定木と呼ばれる、木を逆にしたようなデータ構造を用いて分類と回帰を行います。なお、決定木分析は、ノンパラメトリックな教師あり学習に分類されます。
決定木分析の長所
決定木分析は他の分析手法と比較して、以下の特長があります。
- 入力データから特徴を学習し、決定木と呼ばれる樹木状の構造で学習結果を視覚化でき、ルールをシンプルに表現できる特徴があります。
- 他の多くの手法では、データの標準化 (正規化) やダミー変数の作成を必要とするのに対し、決定木分析では、このような前処理の手間がほとんど不要です。
- カテゴリカルデータ (名義尺度の変数) と数値データ (順序尺度、間隔尺度の変数) の両方を扱うことが可能です。
- ニューラルネットなどのようなブラックボックスのモデルと比較して、決定木はホワイトボックスのモデルだといえ、論理的に解釈することが容易です。
- 検定を行って、作成したモデルの正しさを評価することが可能です。
主要な決定木分析のアルゴリズム
決定木分析には、いくつかの手法が存在します。各手法の違いについて以下に述べます。
ID3
ID3 (Iterative Dichotomiser 3) は、1986 年に、Ross Quinlan によって開発されました。カテゴリカル変数に対して情報量を用いて、貪欲な手法 (≒ あるステップにおいて局所的に評価の高いパターンを選択する) で木を構築します。
C4.5
C4.5 は、ID3 の後継で、数値データの特徴量を動的に離散化するロジックを導入し、全ての特徴量がカテゴリカル変数でなればならないという制約を取り除きました。C4.5 は学習済みの木を if-then で表されるセットに変換し、評価や枝刈り (決定木における不要な部分(枝)を取り除くこと) に用いられます。
C5.0
C5.0 は C4.5 の改善版で、より少ないメモリ消費で動作するよう、パフォーマンスの改善が行われています。
CART
CART (Classification and Regression Trees) は、C4.5 によく類似した手法ですが、数値データで表現される目的変数 (=回帰) にも対応している特徴があります。CART は、ルールセットを計算するのではなく、バイナリ・ツリーを構築します。なお、scikit-learn は最適化したバージョンの CART を実装しています。
scikit-learn に実装されている決定木分析
それでは、実際にデータを用いてモデルを作成して、その評価を行いましょう。scikit-learn では決定木を用いた分類器は、sklearn.tree.DecisionTreeClassifier というクラスで実装されています。
sklearn.tree.DecisionTreeClassifier クラスの書式
|
1 2 3 4 5 |
sklearn.tree.DecisionTreeClassifier(criterion='gini', splitter='best', max_depth=None, min_samples_split=2, min_samples_leaf=1, min_weight_fraction_leaf=0.0, max_features=None, random_state=None, max_leaf_nodes=None, class_weight=None, presort=False) |
sklearn.tree.DecisionTreeClassifier クラスの引数 (詳細)
| criterion (string, 任意) |
分割する際に利用する品質。ジニ係数を利用する “gini” と情報量を示す “entropy” のいずれかを指定。(省略時は “gini”) |
|---|---|
| splitter (string, 任意) |
各ノードにおいて分割を行う方法を選択。”best” (最適) または “random” (ランダム最適) を選択。(省略時は “best”) |
| max_features (int, float, string または None, 任意) |
最適な分割を探索する際に用いる特徴数の最大値。 |
| max_depth (int または None, 任意) |
作成する決定木の深さの最大値。 (省略時は None) |
| min_samples_split (int, 任意) |
サンプルを枝に分割する数の際の枝の数の最小値。 (省略時は 2) |
| min_samples_leaf (int, 任意) |
1 つのサンプルが属する葉の数の最小値。 (省略時は 1) |
| min_weight_fraction_leaf (float, 任意) |
1 つの葉に属する必要のあるサンプルの割合の最小値。 (省略時は 0.0) |
| max_leaf_nodes (int または None, 任意) |
作成する葉の数の最大値。数値を指定した場合は、max_depth が無視されます。 (省略時は None) |
| class_weight (dict, list of dicts, “balanced” または None, 任意) |
各説明変数に対する重み。 (省略時は None) |
| random_state (int, RandomState instance or None, 任意) |
乱数のシードを指定。指定しない場合は、 np.random を利用します。 (省略時は None) |
| presort (bool, 任意) |
高速化の目的で事前に入力データのソートを行うかどうか。 (省略時は False) |
scikit-learn を用いた決定木の作成
今回の分析例では、scikit-learn に付属のデータセット、Iris を利用します。このデータセットには、アヤメのがく片や花弁の幅、長さと、そのアヤメの品種が 150 個体分記録されています。今回は、がく片や花弁の幅、長さを説明変数 (教師データ) 、アヤメの品種を目的変数 (正解データ) として扱い、分類する決定木を作成します。
|
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 |
>>> # データを読み込み >>> from sklearn.datasets import load_iris >>> iris = load_iris() >>> # 説明変数 (それぞれ、がく片や花弁の幅、長さを示します) >>> iris.data array([[ 5.1, 3.5, 1.4, 0.2], [ 4.9, 3. , 1.4, 0.2], [ 4.7, 3.2, 1.3, 0.2], [ 4.6, 3.1, 1.5, 0.2], ... (中略) [ 5.9, 3. , 5.1, 1.8]]) >>> # 目的変数 (0, 1, 2 がそれぞれの品種を表します) >>> iris.target array([0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 2, 2, 2, 2, 2, 2, 2, 2, 2, 2, 2, 2, 2, 2, 2, 2, 2, 2, 2, 2, 2, 2, 2, 2, 2, 2, 2, 2, 2, 2, 2, 2, 2, 2, 2, 2, 2, 2, 2, 2, 2, 2, 2, 2, 2, 2, 2, 2, 2, 2]) |
scikit-learn にて決定木による分類が実装されているクラス、 tree.DecisionTreeClassifier クラスの fit メソッドに、説明変数と目的変数の両方を与え、モデル (=決定木) を作成します。今回は木の深さの最大値として、max_depth=3 を指定しています。
|
1 2 3 4 |
>>> # モデルを作成 >>> from sklearn import tree >>> clf = tree.DecisionTreeClassifier(max_depth=3) >>> clf = clf.fit(iris.data, iris.target) |
次に、作成したモデルに説明変数のみを与え、モデルを用いて予測 (分類) を実行します。
|
1 2 3 4 5 6 7 8 9 10 11 12 |
>>> # 作成したモデルを用いて予測を実行 >>> predicted = clf.predict(iris.data) >>> # 予測結果 >>> predicted array([0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 2, 1, 1, 1, 1, 1, 1, 2, 1, 1, 1, 1, 1, 2, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 2, 2, 2, 2, 2, 2, 1, 2, 2, 2, 2, 2, 2, 2, 2, 2, 2, 2, 2, 2, 2, 2, 2, 2, 2, 2, 2, 2, 2, 2, 2, 2, 2, 2, 2, 2, 2, 2, 2, 2, 2, 2, 2, 2, 2, 2, 2, 2, 2, 2]) |
予測された結果と実際の目的変数を比較し、識別率 (正しく分類された割合) を計算します。計算の結果、約 0.973 (約 97 %) の精度で正しく分類できたことがわかります。
|
1 2 3 |
>>> # 識別率を確認 >>> sum(predicted == iris.target) / len(iris.target) 0.97333333333333338 |
決定木の可視化
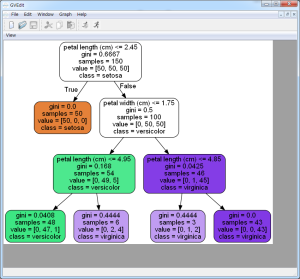
作成した決定木は、DOT ファイルとして、木構造を可視化できるようにエクスポートすることができます。作成した DOT ファイルはオープンソースのグラフ可視化ソフトウェア、 GraphViz を利用して、開くことができます。
本例では引数に、各説明変数の名前の指定 feature_names=iris.feature_names 、目的変数の名前の指定class_names=iris.target_names 、枝に色を塗る filled=True 指定と、枝の角を丸めるrounded=True 指定を行っています。
|
1 2 3 4 |
>>> tree.export_graphviz(clf, out_file="tree.dot", feature_names=iris.feature_names, class_names=iris.target_names, filled=True, rounded=True) |
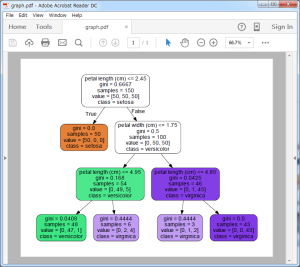
DOT ファイルはやや馴染みのないファイル形式かと思いますが、pydotplus パッケージを利用することで、PDF ファイルとして出力することができます。
|
1 2 3 4 5 6 7 8 9 |
>>> # 作成した決定木を可視化 (pydotplus パッケージを利用) >>> import pydotplus >>> from sklearn.externals.six import StringIO >>> dot_data = StringIO() >>> tree.export_graphviz(clf, out_file=dot_data) >>> graph = pydotplus.graph_from_dot_data(dot_data.getvalue()) >>> # PDFファイルに出力 >>> graph.write_pdf("graph.pdf") |
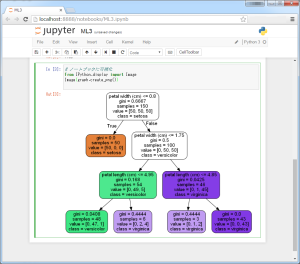
Jupyter や IPython NoteBook を使っている場合は、以下のようにしてノートブック内に可視化することができます。このような方法であれば、作成した決定木を確認しながらモデル作成できるので効率よく分析作業が進められるでしょう。
|
1 2 3 |
>>> # ノートブックに可視化 >>> from IPython.display import Image >>> Image(graph.create_png()) |
参考:1.10. Decision Trees — scikit-learn 0.17.1 documentation