このページでは、三角関数や指数関数、対数関数など、基本的な数学関連の関数の使い方を解説します。
三角関数
正弦関数 (sin(x), サイン) 、余弦関数 (cos(x), コサイン)、正接関数 (tan(x), タンジェント) を求める関数として、それぞれ、np.sin(x) 、np.cos(x) があります。なお、x はラジアンで指定する必要があるため、度はラジアンに変換する必要があります。
サンプルコード
# sin(0) np.sin(0) # sin([0, 1]) np.sin([0, 1]) # cos(1) np.cos(1) # cos([0, 1]) np.cos([0, 1]) # tan(1) np.tan(1) # tan([0, 1]) np.tan([0, 1])
実行結果
>>> np.sin(0) 0.0 >>> np.sin([0, 1]) array([ 0. , 0.84147098]) >>> np.cos(1) 0.54030230586813965 >>> np.cos([0, 1]) array([ 1. , 0.54030231]) >>> np.tan(1) 1.5574077246549023 >>> np.tan([0, 1]) array([ 0. , 1.55740772])
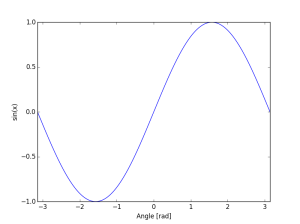
Matplotlib を利用して、サインカーブを出力することもできます。
サンプルコード
import matplotlib.pylab as plt
x = np.linspace(-np.pi, np.pi, 201)
plt.plot(x, np.sin(x))
plt.xlabel('Angle [rad]')
plt.ylabel('sin(x)')
plt.axis('tight')
plt.show()
逆三角関数
逆正弦関数 (インバース・サイン, inverse sin, sin^-1, arcsin)、逆余弦関数 (インバース・コサイン, inverse cosine, cos^-1, arccos)、逆正接関数 (インバース・タンジェント, inverse tangent, cos^-1, arccos) を計算する関数として、np.arcsin(x), np.arccos(x), np.arctan(x) があります。
サンプルコード
# arcsin(1) np.arcsin(1) # arcsin([-1, 0, 1]) np.arcsin([-1, 0, 1]) # arccos(1) np.arccos(1) # arccos([-1, 0, 1]) np.arccos([-1, 0, 1]) # arctan(1) np.arctan(1) # arctan([-1, 0, 1]) np.arctan(-1)
実行結果
>>> np.arcsin(1) 1.5707963267948966 >>> np.arcsin([-1, 0, 1]) array([-1.57079633, 0. , 1.57079633]) >>> np.arccos(1) 0.0 >>> np.arccos([-1, 0, 1]) array([ 3.14159265, 1.57079633, 0. ]) >>> np.arctan(1) 0.78539816339744828 >>> np.arctan([-1, 0, 1]) array([-0.78539816, 0. , 0.78539816])
ラジアン ⇔ 度 の変換
NumPy では、np.radians(x), np.deg2rad(x), np.rad2deg(x) 関数で、弧度法(rad)と度数法 (°) を変換します。なお、np.radians(x), np.deg2rad(x) の 2 つの関数は同じ結果を返します。
サンプルコード
# 度からラジアンへ (np.radians) np.radians(0) np.radians([np.rad2deg(1), 0, 90]) # 度からラジアンへ (np.deg2rad) np.deg2rad(0) np.deg2rad([np.rad2deg(1), 0, 90]) # ラジアンから度へ np.rad2deg(0) np.rad2deg([np.deg2rad(180), 1, 0.5])
実行結果
>>> np.radians(0) 0.0 >>> np.radians([np.rad2deg(1), 0, 90]) array([ 1. , 0. , 1.57079633]) >>> np.deg2rad(0) 0.0 >>> np.deg2rad([np.rad2deg(1), 0, 90]) array([ 1. , 0. , 1.57079633]) >>> np.rad2deg(0) 0.0 >>> np.rad2deg([np.deg2rad(180), 1, 0.5]) array([ 180. , 57.29577951, 28.64788976])
指数関数、対数関数
NumPy には、指数関数として、e(x) を計算する np.exp() があります。
サンプルコード
# e(0) np.exp(0) # e(1) np.exp(1)
実行結果
>>> np.exp(0) 1.0 >>> np.exp(1) 2.7182818284590451
NumPy には、対数関数として以下が定義されています。
- e が底 (Log_e(x)) の
np.log(x) - 2 が底（Log_2(x)）の
np.log2(x) - 10 が底（Log_10(x)）の
np.log10(x)
なお、定数 e は、np.e として定義されています。
サンプルコード
# e を出力 np.e # eが底の指数関数 (Log_e(x)) np.log(1) np.log([1, np.e, np.e ** 2, 0]) # 2が底の指数関数 (Log_2(x)) np.log2(2) np.log2([1, np.e, np.e ** 2, 0]) # 10 が底の指数関数 (Log_10(x)) np.log10(1000) np.log10(1e+10) # 1e+10 = 10,000,000,000
実行結果
>>> np.e 2.718281828459045 >>> np.log(1) 0.0 >>> np.log([1, np.e, np.e ** 2, 0]) array([ 0., 1., 2., -inf]) >>> np.log2(2) 1.0 >>> np.log2([1, np.e, np.e ** 2, 0]):1: RuntimeWarning: divide by zero encountered in log2 array([ 0. , 1.44269504, 2.88539008, -inf]) >>> np.log10(1000) 3.0 >>> np.log10(1e+10) 10.0
剰余
NumPy で剰余 (割り算の余り) を求めるには、np.mod()があります。
サンプルコード
# 配列 [1, 2, 3, 4, 5, 6] の各要素に対する 3 の剰余 np.mod([1, 2, 3, 4, 5, 6], 3)
実行結果
>>> np.mod([1, 2, 3, 4, 5, 6], 3) array([1, 2, 0, 1, 2, 0])
なお、配列を用いない場合は、NumPy を利用せず、Python の関数のみで実現可能です。
サンプルコード・実行結果
>>> 5 % 3 # 5 / 3 = 1 余り 2 2
四捨五入、切捨て、切り上げ
小数を整数に変換する方法としては、いくつかの方法があります。
- 四捨五入
np.round() - 切り捨て
np.trunc() - 切り捨て
np.floor() - 切り上げ
np.ceil() - ゼロに近いほうに丸める
np.fix()
サンプルコード
# 配列 [-1.7, -1.5, -0.2, 0.2, 1.5, 1.7, 2.0] を作成 a = np.array([-1.7, -1.5, -0.2, 0.2, 1.5, 1.7, 2.0]) # 四捨五入 (小数点以下 .5 以上は繰上げ、.5未満は切捨て) np.round(a) # 切り捨て (小数部分を取り除く) np.trunc(a) # 切り捨て (小さい側の整数に丸める) np.floor(a) # 切り上げ (大きい側の整数に丸める) np.ceil(a) # ゼロに近い側の整数に丸める np.fix(a)
実行結果
>>> a = np.array([-1.7, -1.5, -0.2, 0.2, 1.5, 1.7, 2.0]) >>> np.round(a) array([-2., -2., 0., 0., 2., 2., 2.]) >>> np.trunc(a) array([-1., -1., -0., 0., 1., 1., 2.]) >>> np.floor(a) array([-2., -2., -1., 0., 1., 1., 2.]) >>> np.ceil(a) array([-1., -1., -0., 1., 2., 2., 2.]) >>> np.fix(a) array([-1., -1., -0., 0., 1., 1., 2.])
参考までに、配列を用いない場合は、NumPy ではなく、 Python のみで実行可能です。
サンプルコード
import math # 四捨五入 round(1.7) # 切捨て math.floor(1.7) math.trunc(1.7) # 切り上げ math.ceil(1.7)
実行結果
>>> import math >>> round(1.7) 2.0 >>> math.floor(1.7) 1.0 >>> math.trunc(1.7) 1 >>> math.ceil(1.7) 2.0
最大値、最小値
NumPy では、np.maximum , np.minimum 関数を利用して同じ長さの配列から、各要素の最大値、最小値を抽出して新たな配列を作成します。
また、同様の働きをする関数で、np.fmax , np.fmin 関数は、配列の要素に NaN (Not-a-Number) が含まれていた場合に、NaN を無視して数値を出力します。
サンプルコード
# 配列 a, b を定義 a = [1, 4, 5, np.nan] b = [2, 3, 6, 7] # 各要素の最大値、最小値 np.maximum(a, b) np.minimum(a, b) # 各要素の最大値、最小値（NaN を無視する） np.fmin(a, b) np.fmax(a, b) # なお、1つの配列の最大値、最小値は NumPy を使わずにも計算可能です。 max([2, 6, 1, 4, 5, 3]) min([2, 6, 1, 4, 5, 3])
実行結果
>>> a = [1, 4, 5, np.nan] >>> b = [2, 3, 6, 7] >>> np.maximum(a, b) array([ 2., 4., 6., nan]) >>> np.minimum(a, b) array([ 1., 3., 5., nan]) >>> np.fmin(a, b) array([ 1., 3., 5., 7.]) >>> np.fmax(a, b) array([ 2., 4., 6., 7.]) >>> max([2, 6, 1, 4, 5, 3]) 6 >>> min([2, 6, 1, 4, 5, 3]) 1
平方根（ルート）、べき乗 (二乗, 三乗, n乗)
方根（√x）を求める関数として、np.sqrt(x) があります。
サンプルコード
# √16 np.sqrt(16) # 配列を引数に取ることも可能です。例: [√1, √4, √9] np.sqrt([1, 4, 9]) # 配列でなければ、NumPy を用いずに計算できます。 import math math.sqrt(16)
実行結果
>>> math.sqrt(16) 4.0 >>> np.sqrt([1, 4, 9]) array([ 1., 2., 3.]) >>> import math >>> math.sqrt(16) 4.0
複素数
NumPy では複素数の計算にも対応しています。
複素数に関する関数として、複素数の実数部を返す np.real() 、虚数部を返す np.imag() 、共役複素数 (複素共役, 虚数部の符号を逆にした複素数) を返す np.conj() を紹介します。
サンプルコード
# 1+2j の実数部 (=1) を返す np.real(1 + 2j) # [2+3j, 2-3j] の実数部 np.real([2+3j, 2-3j]) # 1+2j の虚数部 (=2) を返す np.imag(1 + 2j) # [2+3j, 2-3j] の虚数部 np.imag([2+3j, 2-3j]) # 1+2j の共役複素数 np.conj(1+2j) # [2+3j, 2-3j] の共役複素数 np.conj([2+3j, 2-3j])
実行結果
>>> np.real(1 + 2j) array(1.0) >>> np.real([2+3j, 2-3j]) array([ 2., 2.]) >>> np.imag(1 + 2j) array(2.0) >>> np.imag([2+3j, 2-3j]) array([ 3., -3.]) >>> np.conj(1+2j) (1-2j) >>> np.conj([2+3j, 2-3j]) array([ 2.-3.j, 2.+3.j])
絶対値
NumPy で絶対値 (負の数は正の数として出力、正の数は正の数として出力) を求めるには、np.absolute()があります。
サンプルコード
# |-2| np.absolute(-2) # |[-1.2, 1.2]| np.absolute([-1.2, 1.2])
実行結果
>>> np.absolute(-2) 2 >>> np.absolute([-1.2, 1.2]) array([ 1.2, 1.2])