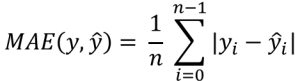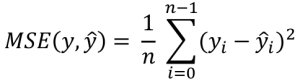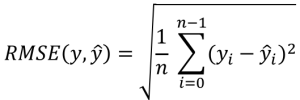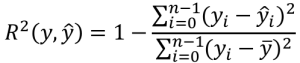本ページでは、Python の機械学習ライブラリの scikit-learn を用いて、回帰モデル (Regression model) の予測精度を評価する方法を紹介します。
回帰モデルの評価にはいくつかの指標があり、本ページでは主要な指標として、MAE, MSE, RMSE, 決定係数の 4 つを紹介します。
平均絶対誤差 (MAE)
平均絶対誤差 (MAE, Mean Absolute Error) は、実際の値と予測値の絶対値を平均したものです。MAE が小さいほど誤差が少なく、予測モデルが正確に予測できていることを示し、MAE が大きいほど実際の値と予測値に誤差が大きく、予測モデルが正確に予測できていないといえます。計算式は以下となります。
(
: 実際の値, 
: 予測値, 
: 件数)
scikit-learn には、sklearn.metrics.mean_absolute_error に計算用のメソッドが実装されており、以下のように利用できます。
|
1 2 3 4 5 |
>>> from sklearn.metrics import mean_absolute_error >>> y_true = [0, 1, 2, 3, 4, 5] >>> y_pred = [0, 1.2, 2.5, 3.4, 4.6, 5.7] >>> mean_absolute_error(y_true, y_pred) 41.666666666666664 |
平均二乗誤差 (MSE)
平均二乗誤差 (MSE, Mean Squared Error) とは、実際の値と予測値の絶対値の 2 乗を平均したものです。この為、MAE に比べて大きな誤差が存在するケースで、大きな値を示す特徴があります。MAE と同じく、値が大きいほど誤差の多いモデルと言えます。計算式は以下となります。
(: 実際の値, : 予測値, : 件数)
scikit-learn には、sklearn.metrics.mean_squared_error に計算用のメソッドが実装されており、以下のように利用できます。
|
1 2 3 4 5 |
>>> from sklearn.metrics import mean_squared_error >>> y_true = [3, -0.5, 2, 7] >>> y_pred = [2.5, 0.0, 2, 8] >>> mean_squared_error(y_true, y_pred) 0.375 |
二乗平均平方根誤差 (RMSE)
MSE の平方根を 二乗平均平方根誤差 (RMSE: Root Mean Squared Error) と呼びます。上記の MSE で、二乗したことの影響を平方根で補正したものです。RMSE は、RMSD (Root Mean Square Deviation) と呼ばれることもあります。計算式は以下となります。
(: 実際の値, : 予測値, : 件数)
scikit-learn には RMSE の計算は実装されていないため、以下のように、np.sqrt() 関数で上記の MSE の結果を補正します。
|
1 2 3 4 5 6 |
>>> from sklearn.metrics import mean_squared_error >>> import numpy as np >>> y_true = [3, -0.5, 2, 7] >>> y_pred = [2.5, 0.0, 2, 8] >>> np.sqrt(mean_squared_error(y_true, y_pred)) 0.61237243569579447 |
決定係数 (R2)
決定係数 (R2, R-squared, coefficient of determination) は、モデルの当てはまりの良さを示す指標で、最も当てはまりの良い場合、1.0 となります (当てはまりの悪い場合、マイナスとなることもあります)。寄与率 (きよりつ) とも呼ばれます。計算式は以下となります。
(: 実際の値, : 予測値, 
: 実際の値の平均値, : 件数)
scikit-learn には、sklearn.metrics.r2_score に計算用のメソッドが実装されており、以下のように利用できます。
|
1 2 3 4 5 |
>>> from sklearn.metrics import r2_score >>> y_true = [3, -0.5, 2, 7] >>> y_pred = [2.5, 0.0, 2, 8] >>> r2_score(y_true, y_pred) 0.94860813704496794 |
参考:
- 3.3. Model evaluation: quantifying the quality of predictions — scikit-learn 0.19.0 documentation
- sklearn.metrics.mean_absolute_error — scikit-learn 0.19.0 documentation
- sklearn.metrics.mean_squared_error — scikit-learn 0.19.0 documentation
- sklearn.metrics.r2_score — scikit-learn 0.19.0 documentation